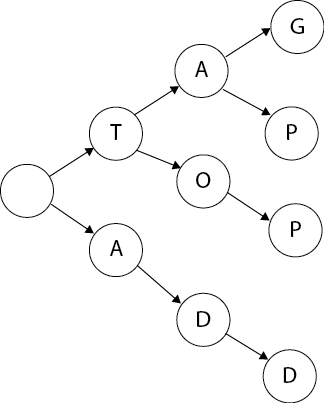
Tries (pronounced ‘try’ or ‘trie’ as in retrieval) is an ordered data structure often used to store strings. It is a type of tree where the decoration on each node represents the position of the element being stored. If we store a string, then a depth first search of the tree to a leaf node will visit characters that make up that string.

Tries are great for super-fast autocomplete search. A breadth first search from any given point in the tree will find an exact match (if it exists), then matches one character away, then two and so on down the tree.

To build a trie we will need a recursively defined node called TrieNode. Let’s take a look at some Ruby code that we will use to build a Trie:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class TrieNode
  def initialize(decoration = '.')
    @decoration = decoration
    @children = {}
  end

  def addLetters(letters)
    addLettersRecursively(letters, letters)
  end

  protected

  def addLettersRecursively(letters, full_word)
    @full_word = full_word and return if letters.size == 0

    first_letter = letters[0]
    @children[first_letter] = TrieNode.new(first_letter) unless @children.has_key?(first_letter)
    @children[first_letter].addLettersRecursively(letters[1..-1], full_word)
  end
end

It has a few instance variables including a decoration and a full_word. We store child relationships by recursively adding new TrieNodes in a children hash peeling off one letter at a time. I could have used a single method for the recursion, but use a addLetters method as a driver for the addLettersRecursively method.

Finding a node in the Trie follows the same pattern as adding letters:

1
2
3
4
5
6

def findNode(letters)
  return self if letters.size == 0

  return @children[letters[0]].findNode(letters[1..-1]) if @children.has_key?(letters[0])
  nil
end

Note that not all nodes in the tree represent member strings that are stored in the Trie. We marked the Trie member nodes with the full_word instance variable above. We need the findNode method for traversals as we will see in a minute.

Now we can implement the Trie itself. It maintains the root node of the tree and has facilities to insert, membership and search:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Trie
  def initialize(words = [])
    @root_node = TrieNode.new
    words.each { |word| @root_node.addLetters(word) }
  end

  def insert(word)
    @root_node.addLetters(word)
  end

  def contains?(word)
    node = @root_node.findNode(word)

    return true if node and node.word
    false
  end

  def search(letters = '')
    words = []
    queue = []
    node = @root_node.findNode(letters)
    return [] if node.nil?
    words << node.word if node.word
    queue << node
    until queue.size == 0 do
      node = queue.shift
      node.children.each do |child_node|
        word = child_node.word
        words << word unless word.nil?
        queue << child_node
      end
    end
    words
  end
end

The search method maintains a list of found words and a queue for a breadth first search of the Trie. We use the shift and << operators to get queue first-in-first-out behavior. Calling search without specifying letters will result in full search for all members in the Trie.

The full source and dictionary is available on GitHub:

https://github.com/nick-aschenbach/trie-autocomplete

Performance

I used a database with about 210K words and did some rough, informal calculations to compare performance between arrays, hashes and my trie implementation. The prefix search is finding all words that started with a substring. Membership is for finding one exact string. Here is what I found:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Prefix search (1000x repetitions)
Trie: 0.034 seconds
Array: 51.3 seconds
Hash: 91.85 seconds

Membership search (100,000x)
Trie: 0.22 seconds
Array: 1580 seconds (estimated: 10,000x took 158 seconds)
Hash: 0.027 seconds

Insertion (100x)
Trie: 88.6 seconds
Array: 0.000023 seconds
Hash: 7.69 seconds

Prefix search performance appears to be efficient compared to arrays and hashes. Membership search appears to be a little slower than hashes. Array membership requires a full search of the array in the worst case O(N). Hash lookup is expected constant time performance. Trie membership is O(M) where M is the number of characters in the string. Insertion performance is very slow (probably due to all of the hashes being generated with this implementation). Typical use of this data structure is for search and insertion should be relatively rare.